私たちが学習・勉強というと、「知識を吸収する」「知識を覚える」「知識を表現する」というように「知識」を中心に考えがちです。

　ところがビジネス界には、それとは少し異なる理論があります。「コルブの経験学習理論（モデル）」がそれです。

　この理論（モデル）は、アメリカの組織行動学者デイヴィッド・コルブによって提唱された学習理論です。この理論（モデル）によれば、学習とは、「具体的な経験（体験する）」→「内省的な観察（振り返る）」→「抽象的な概念化（気づく）」→「能動的な実践（次の計画を立てる）」→（再び）「具体的な経験・・・」という動きであり、その継続が「成長」だというのです。

　つまり、無限に知識を吸収し続けることが「学習・成長」ではなく、自分で自分の体験を振り返り、そこで学んだことを言語化し、次の計画を立てて、再び新しい経験に挑戦していく…この繰り返しこそが人間としての「学習・成長」ということになります。

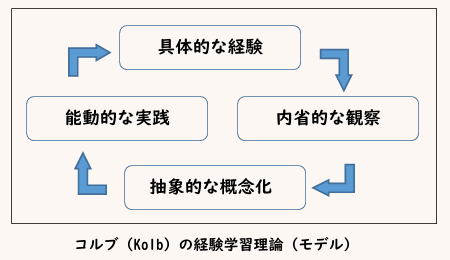
　これを具体的な学習の場面で考えてみると次のようになります。

＜具体的な経験（体験する）＞
実際に算数の問題を解いてみる。例えば、分数の足し算問題に取り組むことで、具体的な課題に直面する。⇒「1/3 + 1/3 + 1/4」を計算する。

＜内省的な観察（振り返る）＞
 問題を解いてみたあと、「どうしてこの答えになったのかな？」と振り返る。間違えた場合には、なぜ間違えたのかを分析することも含まれます。⇒どうして11/12になった？

＜抽象的な概念化（気づく）＞
 問題を解く中で、他の場面にも応用できるルールに気づく。例えば、「分母を最小公倍数で揃える」というルールは、数学的思考の基礎となる。⇒分母を3と4の最小公倍数の12にする。

＜能動的な実践（行動計画をつくる）＞
 学んだルールを次の問題に適用する計画を立てたり、自分で新しい問題を作成して解いてみたりする。⇒「1/2 + 1/3 + 1/6」だったら分母はいくつにそろえるのか？

　そして、このサイクルを繰り返すことで、算数（分数計算）の理解力や解く力がどんどん高まっていくというイメージです！

　考えることが楽しくなると、次のような問題を考えてみるのもよいかもしれません。

　問題：ピザを３人で分けました。２人はそれぞれ1/3ずつ食べ、もう1人は1/4食べました。残りのピザはどれだけですか？

　このような身近な場面を使って考える力を育むことが、算数をさらに楽しくする鍵です！

　さて、答えは分かりましたか？（ヒントはこの文章中にありますよ。それぞれの食べた量を足して、残りを計算してみてください。）

◎主に参考とした本：デイヴィッド・コルブ、 ケイ・ピーターソン、 中野眞由美『最強の経験学習』辰巳出版　2018年
◎主に参考とした本：松尾睦『職場が生きる 人が育つ 「経験学習」入門』ダイヤモンド社  2011年